High Frequency Measurements Web Page
Douglas C. Smith

 Address:  P. O. Box 1457, Los Gatos, CA 95031
 TEL:      800-323-3956/408-356-4186
 FAX:      408-358-3799
 Mobile:   408-858-4528
 URL:      www.dsmith.org
 Email:    doug@dsmith.org


Technical Tidbit - October 2003
Heisenberg and Signal Measurements
(A variation on the Uncertainty Principle)

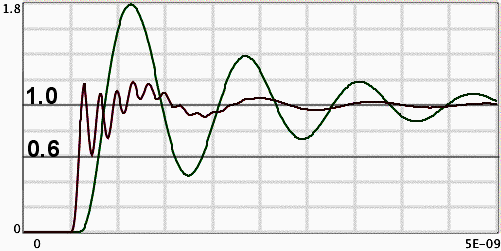
  Measured and actual voltage from source
Figure 1. Actual Node Voltage (red on left) and Probe Response (green, delayed) Without Damping Resistor
(vertical scale = 0.2 Volt/div)
(horizontal scale = 500 ps/div)

Abstract: Heisenberg's Uncertainty Principle might be adapted in the context of signal measurements to say that one cannot measure a voltage at a node without affecting it. Simulation data is presented to show that under realistic conditions, active probes without damping resistors can significantly affect the signal to be measured. The result can be more serious than just signal loading.

Discussion: Probing a signal at a node in a circuit can have significant effects that can go beyond simple loading effects. This is especially true at today's faster signal rates and frequencies. Although a probe can be checked against a known waveform to see its impulse response, a more difficult task is to determine the probe's affects on the original signal. For this task, computer simulations of the probe and circuit can lend insight into how the signal may be changed by the scope probe.

Active probes before about 2  years ago had a mostly capacitive input impedance, generally one picofarad or less. The problem is that even that capacitance forms a resonant circuit and causes measurement error and circuit loading. Recently, active probe designs use a damping resistor on the order of 100 to 200 Ohms in series with the probe tip. This lowers the Q of the tuned circuit consisting of the probe capacitance and the inductance of the probe connections and circuit being measured.  Using MI-SUGAR (Spice with a graphical interface running on Mac OS X) and a model of an active probe published by the manufacturer, simulations were performed to see how use of the damping resistor affects the probe's interaction with the circuit to be measured.

Figure 1 shows simulation results of probe response (delayed signal in green) and the actual voltage at the measured node (red on left) for a 1 Volt source having an impedance of 25 Ohms in series with 5 nH without the probe damping resistor. The source resistance was chosen to represent a gate output resistance and the inductance to represent nominal package inductance. Many modern chip packages have signal path inductances ranging from 2 to 8 nH*. The risetime of the applied step is 100 ps.

The probe model used in the spice simulation is a manufacturer's multi-element model of a 4 GHz active probe fitted with a 5 cm extension adapter that included a damping resistor at the tip of about 200 Ohms. The simulation modeled the probe's connections and input circuitry, but not the probe amplifier response for simplicity. For the plots in Figure 1, the damping resistor was removed. Without the damping resistor, the probe's input impedance and response is similar to active probe designs that do not include a damping resistor. The probe response has a familiar overshoot and ringing that is common with even short probe connections on many active probes. In this case the probe response overshoots 80% to 1.8 volts and rings just under 1 GHz for several cycles. The probe response in Figure 1 agrees well with measured results on active probes without damping resistors, thus helping to verify the simulation results.

However, the important detail in Figure 1 is the actual signal on the node during the measurement, the red trace starting on the left. With the 25 Ohm+5nH signal source used in the simulation,  the node voltage fell to a value of about 0.6 Volt, low enough to possibly cause signal integrity problems. Both the peak-to-peak amplitude and the period of the fast oscillations are sensitive to the amount of source inductance, but even a few nH of inductance can be a problem. Of course, the node voltage cannot be observed on a real circuit because it is changed by probing it, but the simulation suggests a real possibility of problems caused by an active probe without a damping resistor at the tip.

Figure 2 shows the probe response (delayed green trace) and node voltage (red trace starting to left) when the ~200 Ohm damping resistor was present in the circuit. There is no overshoot in the probe response and the node voltage was much better behaved, dipping only about 10% and not exhibiting any ringing. Notice that the risetime of the probe response is about 300 ps, more indicative of a 1 GHz bandwidth than the 4 GHz bandwidth the probe actually is capable of. This is due to the inductance of the 5 cm probe extension. Although the damping resistor can remove the overshoot and ringing as well as reduce effects in the measured circuit, it cannot restore bandwidth lost due to inductance in the probe connections. Probe connections should be kept as short as possible for this reason and other reasons. That being said, the waveforms in Figure 2 are very good compared to those in Figure 1. Only passive probes can achieve better performance in terms of tolerance to probe connection inductance.


  Node and Measured Voltage With Damping Resistor
Figure 2. Actual Node Voltage (red on left) and Probe Response (green, delayed) With Damping Resistor
(vertical scale = 0.2 Volt/div)
(horizontal scale = 500 ps/div)

Summary and Conclusion: Active probes, or any type of scope probe for that matter, can have significant effects on the measured signal that are quite distinct from the response of the probe itself. Heisenberg's principle reinvented! Active probes should always have damping resistance either
built in or added and probe connections should be kept as short as possible. These days, that means very short indeed.

Other articles on this website covering probing effects include:

Equipment used in this article includes:

* Inductance numbers from a private conversation with Michael King.

Top of page
Home

Questions or suggestions? Contact me at doug@dsmith.org
Copyright © 2003 Douglas C. Smith